
There are three methods that are often used in solving quadratic equations, namely factoring, complete perfect square, and use the formula abc (quadratic formula). In seeking to resolve quadratic equations, we usually try memfaktorkannya first. If we encounter obstacles, then we use the formula abc or complete perfect square. This time we will prove the formula abc in other ways, though the same principle, that is, change the left side will be a perfect square shape.
So that the left side will be converted into the shape of squares, the coefficients of 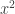 should form squared. Previously we divide the equation by a, so that we gain coefficient 1 which is the simplest quadratic numbers. In proof of this, we multiply the equation with 4a, in order to obtain
should form squared. Previously we divide the equation by a, so that we gain coefficient 1 which is the simplest quadratic numbers. In proof of this, we multiply the equation with 4a, in order to obtain  coefficients
coefficients 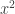 .
.
Cut both sides with 4ac, so.
Add  on both sides.
on both sides.
Change the left side will be a perfect square shape.
Pull the root to both sides.
Cut both sides with b.
For both sides by 2a.
Proven.




